Have you ever manipulated sensitive data for business purposes ? If the answer is yes, we hope that you did not leak it. In the era of big data, companies collect massive amounts of sensitive data to improve their services. This data should be manipulated cautiously. Anonymization was once considered as a solution to address privacy issues. However, it has been shown that anonymized data sharing can still link to privacy leakage.

Protecting databases from sharing

One of the most popular examples of re identification is the Netflix watch history deanonymization. Back in 2006, Netflix organized a movie recommendation contest with a prize of 1 million dollars. As part of this competition, the company released a dataset that contained the watch history of around 500,000 users. Netflix believed that removing all personally identifiable information such as names, coordinates and aliases from the dataset and replacing them with IDs would sufficiently safeguard their customers' privacy. However, a group of researchers discovered that an individual's watch history could almost uniquely identify each user and they used this information to link the watch histories to profiles in the IMdB database.

One might ask, "Why should we worry about the privacy of something as seemingly innocuous as our watch history?" The answer is that the issue runs much deeper. The Netflix case study merely demonstrates that anonymization techniques do not necessarily ensure privacy protection. In future studies, similar techniques could potentially expose much more sensitive information, such as one's religious beliefs, political views, or daily routines. As such, it is crucial to consider the broader implications of data privacy breaches and take necessary measures to prevent them. In other words, simply classifying data as anonymous does not necessarily guarantee complete privacy protection and it is important to treat all data as sensitive because it is impossible to predict the prior knowledge a potential attacker might possess.

Protecting algorithms from attacks (membership inference attacks)

If you are a data scientist or ML engineer, you might think that privacy concerns regarding data releases are not applicable to you, as you release ML models rather than datasets. However, it is crucial to understand that models are themselves based on data. In fact, a neural network model can be viewed as a mathematical function of the training data. Although this function may not be reversible, it does not necessarily preclude the possibility of privacy breaches. Membership inference attacks take advantage of this vulnerability by extracting information about the original training set through the model itself.

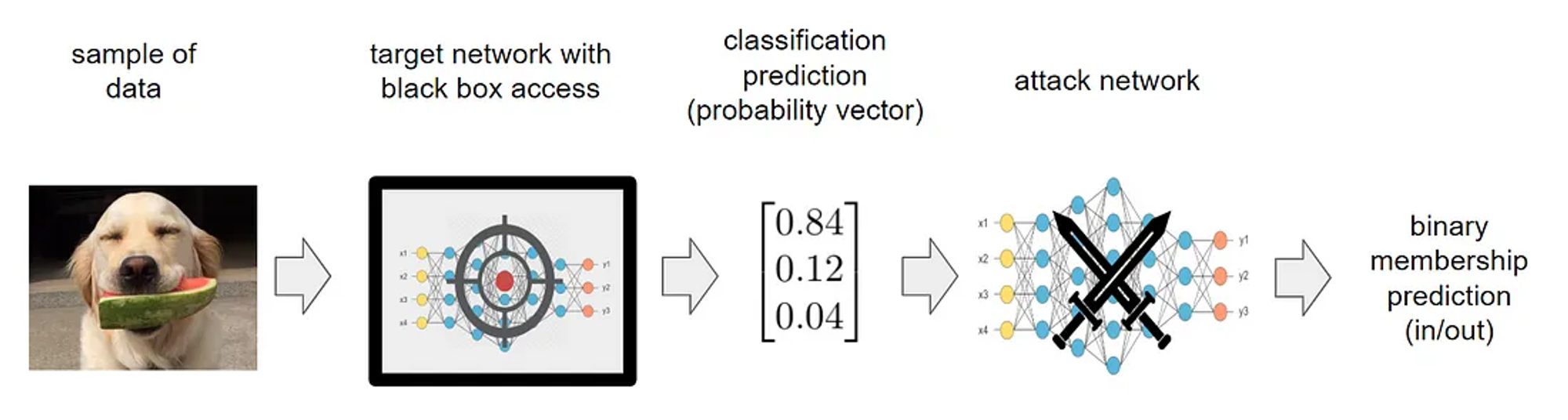
Then, are we doomed to not share anything about models ?

Differential Privacy to protect algorithms

Overview of DP, from intuition to applications

Thankfully, a mathematical framework called 'differential privacy' designed by Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam Smith in 2006, has been designed to address privacy concerns in randomized algorithms. We define a randomized algorithm as an algorithm which output depends on its input (here, a database $x$) and some random intrinsic variable. This framework is specifically applicable to randomized algorithms because privacy guarantees are obtained by adding some randomness to the original algorithm. The idea behind differential privacy is to analyze databases in a way that prevents algorithms from learning anything about specific individuals while retaining useful information about the statistical properties of the general population. It is important to understand what view of privacy is protected by differential privacy. For example, when conducting a study to determine if smoking causes cancer, an insurance company analyzing the study might infer whether an individual participated or not in the study, then if she smokes or not and increase their insurance rates, causing harm. However, if the study's only conclusion is that smoking causes cancer, with no ability to identify whether a specific individual participated, there would be no privacy breach under the differential privacy framework. This view of privacy is protected under differential privacy, which ensures that outputs are minimally dependent of whether any particular individual participated in the study, preventing any potential privacy harm. Specifically, a differentially private randomized algorithm that receives a dataset as input should produce nearly the same result whether or not an element is added or removed from the dataset.

Before delving into the mathematical definitions of differential privacy, it is important to note some remarkable properties of this framework. Differential privacy is a powerful tool that provides several advantages over traditional approaches to privacy. For instance, it is model-free with respect to potential attackers, meaning that regardless of their prior knowledge or post-processing techniques, the output of the randomized algorithm will not significantly change their knowledge of the dataset. This means there is no need to model the objective or capacity of the attacker anymore. The level of privacy loss is tracked through precise bounds that depend on the "privacy budget” $(\varepsilon,\delta)$, a parameter characterizing a differentially private algorithm. The lower the value of $\varepsilon$ and $\delta$, the stronger the privacy guarantees are. Moreover, differential privacy comes with a rigorous privacy tracking and has ‘good’ properties with respect to composability.

Standard differentially private mechanisms mechanisms are particularly effective for simple queries, such as numerical queries. To privatize numerical queries, additive noise privatization schemes are frequently employed. These schemes operate by selecting a distribution $\mathcal{Q_\varepsilon}$ and outputting a noised result of the numerical query $f$ on the database $x$ in question :  $y \sim f(x) + \mathcal{Q_\varepsilon}$ . It has been shown that $Var(\mathcal{Q_\varepsilon})$ decreases as $\varepsilon$ increases, indicating that as more noise is added to the query, the privacy budget becomes tighter, resulting in better privacy guarantees. This creates a tradeoff between privacy and utility when conducting analysis using differentially private mechanisms. These mechanisms are useful for simple queries but data scientists deal with more complicated cases, such as training and sharing machine learning models. Fortunately, there are algorithms specifically designed to enable the training of machine learning algorithms in a differentially private manner. The differentially private stochastic gradient descent algorithm (DPSGD) is one of them.  However, as with numerical queries, privacy protection comes at a cost. There is a tradeoff between privacy and utility that is evaluated empirically and is often difficult to anticipate.

Formal definition of differential privacy and privatization mechanisms

The main concepts and theorems from this section are drawn from “Algorithmic foundations of Differential Privacy” by Cynthia Dwork and Aaron Roth [1].

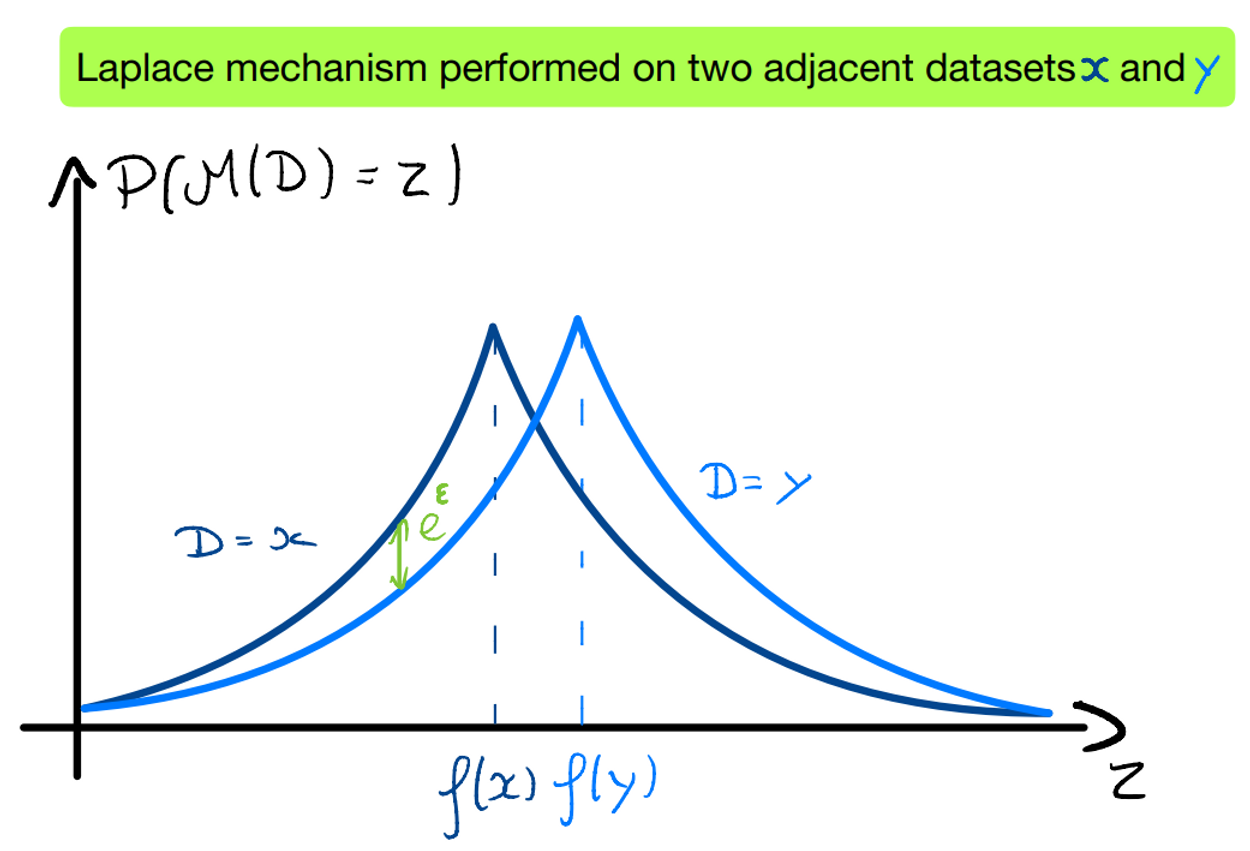
Mathematically, differential privacy bounds the distribution of the randomized algorithm when given in inputs two similar datasets. Here, we define the notion of ‘similarity’ in differential privacy :

Let $\mathcal{X}$ be the set of values that an element from the database can take. We introduce the histogram representation of a given database $x \in \mathbb{N}^{\mathcal{X}}$ with each $x_i$,  $i \in \mathcal{X}$ counting the number of times the element $i$ appears in $x$. Two databases $x$ and $y$ are adjacent if they are equal except for one line : $\exists \; i_0 \in \mathcal{X} \text{ such as } x_{i_0} \in \{y_{i_0}+1,\; y_{i_0}-1 \} \text{ and } \forall\; i \in \mathcal{X} \text{ such as } i \neq i_0, \; x_i = y_i$ .

Differential privacy bounds the privacy loss : given a randomized algorithm $\mathcal{M}$, two adjacent databases $x, y$ and an observable outcome  $\xi \sim\mathcal{M}(x)$, we define the privacy loss as : $\mathcal{L}^\xi_{\mathcal{M}(x),\mathcal{M}(y)} = ln\left[\frac{P \left[\mathcal{M}(x)=\xi \right]}{P \left[\mathcal{M}(y)=\xi \right]}\right]$

If this loss is positive, $\xi$ is more likely under $x$ than $y$. Conversely, if it is negative, $\xi$ is more likely under $y$ than $x$. The magnitude of this loss highlights how much one event is more likely than the other. Differential privacy aims to limit this ratio to a certain threshold.

We introduce $(\varepsilon,\delta)$-differential privacy, or $(\varepsilon,\delta)$-DP.

Definition ($(\varepsilon,\delta)$-differential privacy) :A random mechanism $\mathcal{M}$ of domain $\mathbb{N}^{\mathcal{X}}$ is $(\varepsilon, \delta)$-DP if for all $S \subset Im(\mathcal{M})$ and $x,\, y \in \mathbb{N}^{\mathcal{X}}$ two adjacent databases :$P \left[\mathcal{M}(x)\in S\right] \leq e^\varepsilon P \left[\mathcal{M}(y)\in S\right] + \delta$$(\varepsilon,\delta)$ is the privacy budget.

Interpretation of differential privacy:

With the definition of privacy loss as above, if $\mathcal{M}$ satisfies $(\varepsilon,\delta)$-DP, it holds :$P\left[\left|\mathcal{L}^\xi_{\mathcal{M}(x),\mathcal{M}(y)}\right| \leq \varepsilon\right] \leq 1-\delta$

While $\varepsilon$ quantifies the indistinguishability of the queries on two adjacent databases, $\delta$ introduces a failure probability in the process. $(\varepsilon,\delta)$-DP is a relaxation of $\varepsilon$-DP. $\delta$ quantifies how often the assumption of $\varepsilon$-DP will not hold.

In order to get satisfying privacy guarantees, $\delta$ should be sufficiently small. Values of $\delta$ in the order of $1/\|x\|_1$ are really dangerous as they induce a privacy failure. In fact, the query "select in a database x a record of $\delta\|x\|_1$ elements and output it" is $(0,\delta)$-DP ! For $\delta \geq 1/\|x\|_1$, the algorithm discloses more than one element from the dataset while holding differential privacy guarantees. The privacy breach here is obvious. For practical applications, $\delta$ should be less than the inverse of any polynomial in the size of the database. We usually take $\delta \ll 1/\|x\|_1$.

Differentially private mechanisms and applications to ML:

Differential privacy is a mathematical framework, not an algorithm. It means that, for one given task and one privacy budget, there will be multiple mechanisms achieving the task while guaranteeing differential privacy for the fixed privacy budget. The challenge is finding the mechanism which preserves the most the utility of data. Let us introduce the main mechanisms for DP on basic queries.

Laplace and gaussian mechanisms : additive privatization schemes

Additive privatization schemes are a common approach to preserving the privacy of numerical queries. The main idea is to add noise to the output of the query, resulting in a noisy response that still preserves the privacy of the underlying dataset. Examples of such mechanisms include the Laplacian and Gaussian mechanisms, which add Laplace and normal noise, respectively, to the output of the numerical query. The amount of noise added is determined by the sensitivity of the query, which is defined as the maximum difference between the outputs of the query for two adjacent datasets. By tuning the privacy budget based on the sensitivity of the query, these mechanisms can achieve a desired level of privacy while minimizing the loss of utility.

Composability

Another property differential privacy should have is some form of stability for composition of differentially private algorithms. However, intuitively, the more DP algorithms we run, the weaker privacy guarantees become. Let $f : \mathbb{N}^{\mathcal{X}} \to \mathbb{R}^k$ be a numerical query and  $x \in \mathbb{N}^{\mathcal{X}}$ a dataset. Then, the Laplace mechanism $ML(\cdot, f, \varepsilon)$ ensures $\varepsilon$-DP for f. If we run $n$ times the same mechanism $(f_1,\dots,f_n)=(f,\dots,f)$, we have for a given dataset $x$ :$\frac{1}{n}\sum_{i=1}^{n}ML(x, f_i, \varepsilon) = f(x) + \frac{1}{n}\sum_{i=1}^{n}\left(Y_1^{i}, \dots, Y_k^{i}\right)\to f(x) \; \; p.s.$by the law of large numbers.

It means that if we run an infinite time the same differentially private algorithm, there is no more privacy guaranties.

This privacy degradation is quantified through composition theorems :

Theorem (simple composition): Let $\mathcal{M}_1 : \mathbb{N}^{\mathcal{X}} \to \mathcal{R}_1$ be a $(\varepsilon_1,\delta_1)$-DP algorithm, and let $\mathcal{M}_2 : \mathbb{N}^{\mathcal{X}} \to \mathcal{R}_2$ be a  $(\varepsilon_2,\delta_2)$-DP algorithm. Then their combination, defined to be $ \mathcal{M}{1,2} = \left(\mathcal{M}{1},\mathcal{M}_{2}\right)$ is $(\varepsilon_1+\varepsilon_2,\delta_1+\delta_2)$-DP.

This theorem provides a nearly optimal upper limit for the privacy budget, but it has a critical drawback: it scales linearly with the number of algorithms run on the dataset, resulting in rapid privacy degradation. Nevertheless, repeated differentially private queries are frequently composed on the same dataset. $k$-fold adaptive composition is a method that involves performing $k$ private mechanisms on the same dataset. It involves observing the outputs of one randomized algorithm and using that information to choose the next one. This approach enables an adversary to choose a mechanism to apply to the dataset and adjust it based on the output of previous mechanisms. This type of composition is prevalent in deep learning.

Theorem (advanced composition): For all $\varepsilon, \delta, \delta' \geq 0$, the class of $(\varepsilon,\delta)$-DP mechanisms satisfies $(\varepsilon', k\delta + \delta')$-DP under $k$-fold adaptive composition for$\varepsilon' = \sqrt{2kln(1/\delta')\varepsilon}+k\varepsilon(e^\varepsilon-1)$

This composition scales with $\sqrt{k}$ for $\varepsilon$ small enough, which is better than the linear scaling of the simple composition theorem. It is crucial in deep learning where differentially private models are trained by combining a large number of differentially private steps.

‍

Differential privacy applied to machine learning

Differentially private stochastic gradient descent has been introduced in “Deep Learning with Differential Privacy” by Abadi et al. in 2016 [2]. In this section, we make a brief introduction of the algorithm. The objective is noising and clipping the gradients during the training. This algorithm achieves differential privacy guarantees and the privacy budget can be tracked for each step of the training. This algorithm comes with a tradeoff between privacy and utility. Here below is the state of the art [3] of the performances that can be achieved by DP SGD for image classification algorithms :

Differentially private synthetic data

A last idea to protect algorithms from privacy leakage is differentially private synthetic data. This method involves using a differentially private model to generate synthetic data from the original database, providing the flexibility to use it for any analysis while achieving the desired privacy protection. At Craft AI, we believe that well-designed differentially private synthetic data models can offer the best solution to many privacy issues, as the generated data can be shared freely among users, allowing the use of the data for any analysis, even by those not familiar with privacy concepts. Multiple libraries are available for generating tabular synthetic data, including The Synthetic Data Vault (https://github.com/sdv-dev/SDV) and synthcity (https://github.com/vanderschaarlab/synthcity), which provide their own models that must be trained privately to ensure privacy guarantees.

Differential privacy libraries

This section provides an overview of the primary differential privacy implementing libraries. Each library highlighted here is either the most widely used library for its respective machine learning framework or is particularly noteworthy for its ease of use.

1. Opacus - MetaMeta's Opacus is a PyTorch-compatible library for differential privacy that is particularly noteworthy for its simplicity. With this library, differentially private models can be trained with minimal code modifications, and the privacy budget is well-tracked. Additionally, the framework can easily adapt to a variety of models. Furthermore, the library is open-source and is actively maintained. (link: https://github.com/pytorch/opacus)

2. Tensorflow Privacy - GoogleTensorFlow Privacy is the Tensorflow counterpart to PyTorch's Opacus. It is a Python library that provides TensorFlow optimizer implementations for training machine learning models with differential privacy. The library comes with a lot of tutorials and is still developing.

‍

3. Smartnoise Synth - OpenDPSmartnoise Synth is a privacy library that provides specialized models for differentially private synthetic data generation. Unlike other libraries that focus on training models with differential privacy, Smartnoise Synth is dedicated to generating synthetic data that preserves the privacy of the original dataset. The library is easy to use and well-documented, making it a popular choice for generating synthetic data with differential privacy guarantees.

‍

4. Diffprivlib - IBMDiffprivlib is another privacy library that offers its own models as well as a range of differentially private mechanisms, similar to Smartnoise Synth. The library provides an easy way to benchmark differentially private models, making it a useful tool for data scientists working with sensitive data.

‍

Conclusion

At Craft AI, we consider differential privacy as a crucial component for protecting algorithms and privacy analysis, and we encourage data scientists and machine learning engineers to develop models and solutions that take into account the risks associated with sensitive data manipulation. By designing differentially private models and synthetic data, we can mitigate the risks associated with machine learning models and databases.

‍

References :

[1] Cynthia Dwork, Aaron Roth, The Algorithmic Foundations of Differential Privacy, 2006.
[2] Martın Abadi, Andy Chu, Ian Goodfellow, H. Brendan McMahan, Ilya Mironov, Kunal Talwar, Li Zhang, Deep Learning with Differential Privacy, 2016
[3] Soham De, Leonard Berrada, Jamie Hayes, Samuel L. Smith, Borja Balle, Unlocking High-Accuracy Differentially Private Image Classification through Scale, 2022

‍

Written by Clément Pierquin